一文读懂BiLSTM+CRF实现命名实体识别¶
BiLSTM + CRF是一种经典的命名实体识别(NER)模型方案,这在后续很多的模型improvment上都有启发性。如果你有了解NER任务的兴趣或者任务,或者完全出于对CRF的好奇,建议大家静心读一读这篇文章。
本篇文章会将重点放到条件随机场(CRF)上边,因为这是实现NER任务很重要的一个组件,也是本篇文章最想向你推荐的特色。但是如果你 对长短时记忆网络(LSTM)也不是很熟悉,那你也不用担心,笔者会去解释LSTM的用法,它的输入和输出等等内容,以保证你可以顺畅的读下去,领悟到这个模型的精髓。
整篇文章内容将这样进行组织:
回归CRF建模原理本身
2.1 线性CRF的定义
2.2 发射分数和转移分数
2.3 建模CRF的损失函数
2.4 单条路径的分数计算
2.5 全部路径的分数计算
2.6 CRF的Viterbi解码
1. 使用BiLSTM+CRF实现NER ¶
为方便直观地看到BiLSTM+CRF是什么,我们先来贴一下BiLSTM+CRF的模型结构图,如图1所示。
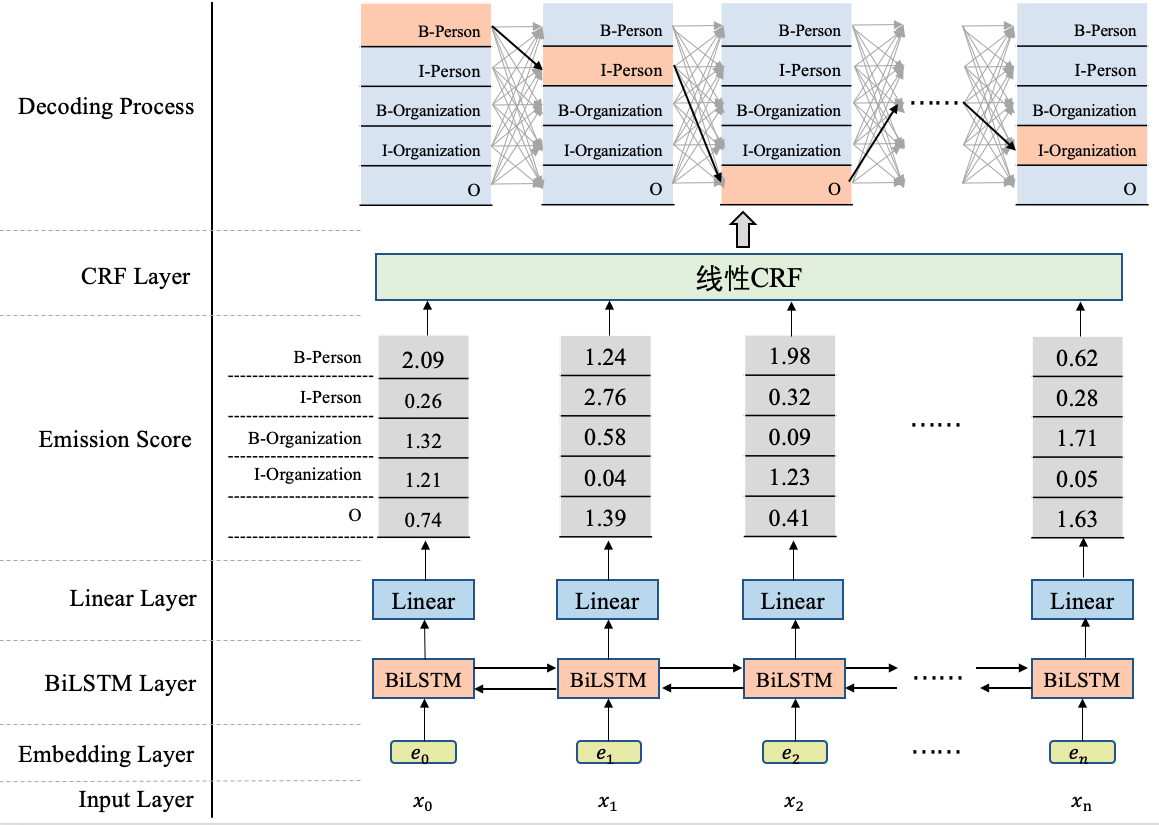
从图1可以看到,在BiLSTM上方我们添加了一个CRF层。具体地,在基于BiLSTM获得各个位置的标签向量之后,这些标签向量将被作为发射分数传入CRF中,发射这个概念是从CRF里面带出来的,后边在介绍CRF部分会更多地提及,这里先不用纠结这一点。
这些发射分数(标签向量)传入CRF之后,CRF会据此解码出一串标签序列。那么问题来了,从图1最上边的解码过程可以看出,这里可能对应着很多条不同的路径,例如:
B-Person, I-Person, O, …, I-Organization
B-Organization, I-Person, O, …, I-Person
B-Organization, I-Organization, O, …, O
CRF的作用就是在所有可能的路径中,找出得出概率最大,效果最优的一条路径,那这个标签序列就是模型的输出。
我们来总结一下,使用BiLSTM+CRF模型架构实现NER任务,大致分为两个阶段:使用BiLSTM生成发射分数(标签向量),基于发射分数使用CRF解码最优的标签路径。
2. 回归CRF建模原理本身¶
本节将开始聚焦在CRF原理本身进行讲解,力图为读者展现一个清楚明白,基础本质的CRF。那现在开始这趟学习之旅吧,相信你一定会有所收获。
2.1 线性CRF的定义¶
通常我们会使用线性链CRF来建模NER任务,所以本实验将聚焦在线性链CRF来探讨。那什么是线性链CRF呢,我们来看下李航老师在《统计学习方法》书中的定义:
设\(X=[x_1, x_2, ..., x_n],Y=[y_1, y_2, ..., y_n]\) 均为线性链表示的随机变量序列,若在给定随机变量序列的\(X\)的条件下,随机变量序列\(Y\)的条件概率分布\(P(Y|X)\)构成条件随机场,即满足马尔可夫性:
则称\(P(Y|X)\)为线性链条件随机场。
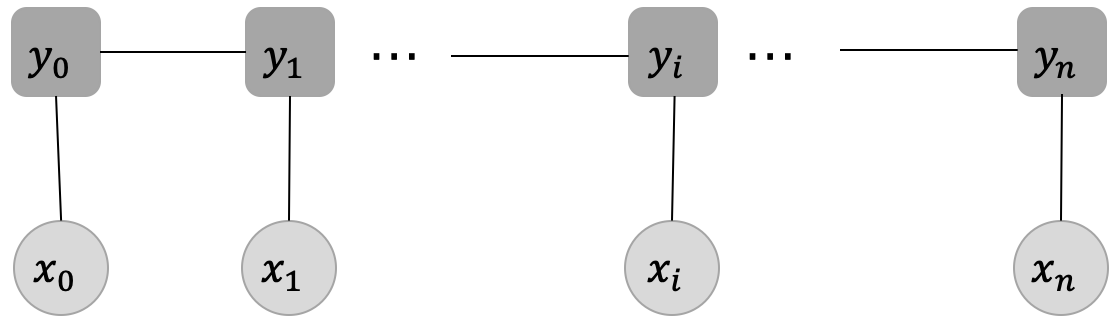
同学们看到这个定义,或许会有些疑惑,但是不用着急,我们来探讨下这个定义。图2展示了一种经典的线性链CRF的结构图,从这张结构图来理解这个定义,主要包含两个点:
确保输入序列\(X\)和输出序列\(Y\)是线性序列
每个标签\(y_i\)的产生,只与这些因素有关系:当前位置的输入\(x_i\),\(y_i\)直接相连的两个邻居\(y_{i-1}\)和\(y_{i+1}\),与其他的标签和输入没有关系。
这样的定义,其实帮助我们减小了建模CRF的代价。
2.2 发射分数和转移分数¶
上边我们探讨了线性链CRF的定义以及它的一种经典图结构,接下来我们继续回到我们建模的命名实体任务上来。
在图2中,\(x=[x_0, x_1, ... , x_i, ... , x_n]\)代表输入变量,对应到我们当前任务就是输入文本序列,\(y=[y_0, y_1, ..., y_i, ..., y_n]\)代表相应的标签序列,
其中,每个输入\(x_i\)均对应着一个标签\(y_i\),这一步对应的就是发射分数,它指示了当前的输入\(x_i\)应该对应什么样的标签;在每个标签\(y_i\)之间也存在连线,它表示当前位置的标签\(y_i\)向下一个位置的标签\({y_{i+1}}\)的一种转移。举个例子,假设当前位置的标签是”B-Person”,那下一个位置就很有可能是”I-Person”标签,即标签”B-Person”向”I-Person”转移的概率会比较大。
这里我们带出了建模CRF过程中两个重要的概念:发射分数和转移分数,下边我们来看看他们是什么。
2.2.1 发射分数¶
前边我们在第2节已经提到过发射分数了,即BiLSTM后产生的标签向量。如果大家对这部分内容已经很熟悉,完全可以跳过这部分。图3以矩阵的形式展示了发射分数的生成过程。
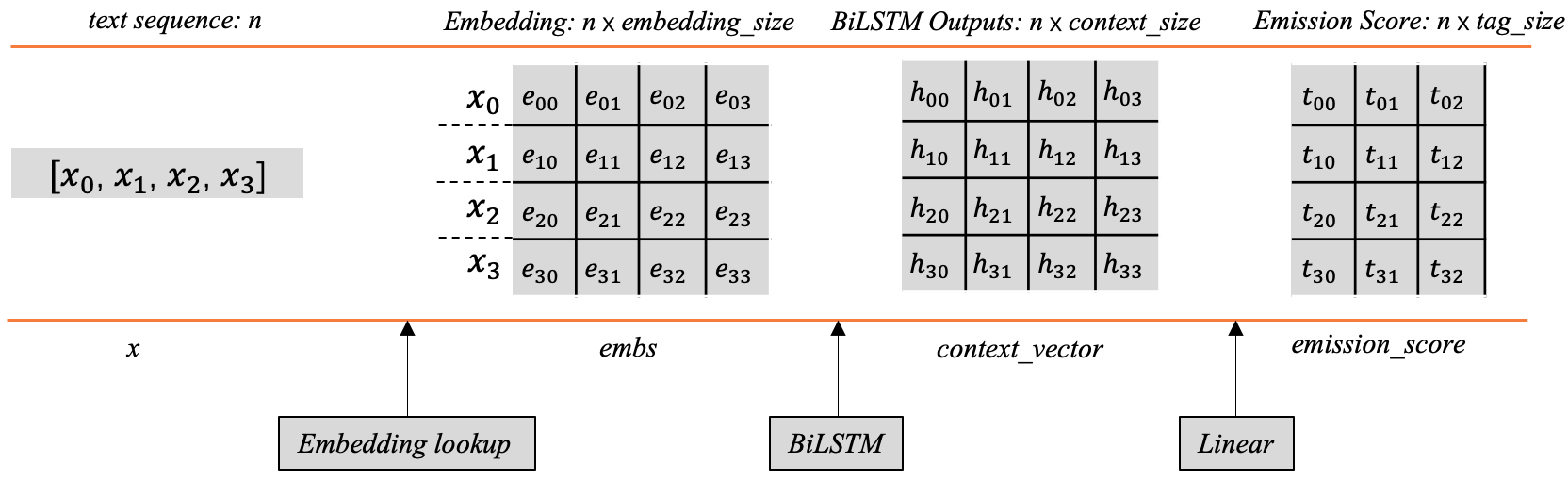
当给定的文本序列\(x=[x_1, x_2, x_3,..., x_n]\)映射为对应词向量之后,将会得到一个shape为\([n, embedding\_size]\)的词向量矩阵\(embs\),其中每对应一个字词(图5样例只使用了4个词),例如\(x_0\)对应的词向量是\([e_{00}, e_{01}, e_{02}, e_{03}]\)。
然后将\(embs\)传入BiLSTM后,每个词的位置都会产生一个上下文向量,所有的向量组合之后会得到一个向量矩阵\(context\_vector\),其中每行代表对应单词经过BiLSTM后的上下文向量。
这里的每个位置的上下文向量可以用来指导当前位置应该输出的标签信息,但这里有个问题,这个输出向量的维度并不是标签的数量,它不能直接用来指示应该输出什么标签。一般的做法是在后边加一层线性层,将这个上下文向量的维度映射为标签的数量,这样的话就会生成前边所讲的标签向量,其中的每个元素分别对应着相应标签的分数,根据这个分数可以用来指导最终标签的输出。
具体地,线性层这里只是做了这样的一个线性变换:\(y = XW+b\),显然,这里的\(X\)就是\(context\_vector\), \(y\)是相应的\(emission\_score\),\(W和b\)是线性层的可学习参数。 前边提到,\(context\_vector\)的shape为\([n,context\_size]\),那么线性层的\(W\)的shape应该是\([context\_size, tag\_size]\),经过以上公式的线性变换,就可以得到发射分数\(emission\_score\),其中每个字词对应一行的标签分数(图3中只设置了三列,代表一共有3个标签),例如,\(x_0\)对第一个标签的分数预测为\(t_{00}\),对第二个标签的分数预测为\(t_{01}\),对第三个标签的分数预测为\(t_{02}\),依次类推。
2.2.2 转移分数¶
下面我们来聊聊转移分数,这个转移分数表示一个标签向另一个标签转移的分数,分数越高,转移概率就越大,反之亦然。图4展示了记录转移分数的矩阵。
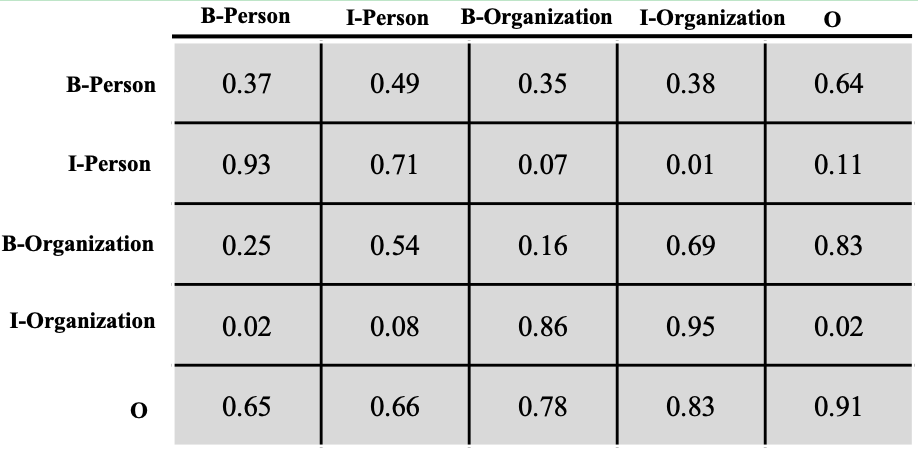
让我们从列到行地来看下这个转移矩阵\(T\),B-Person向I-Person转移的分数为0.93,B-Person向I-Organization转移的分数为0.02,前者的分数远远大于后者。I-Person向I-Person转移的概率是0.71,I-Organization向I-Organization转移的分数是0.95,因为一个人或者组织的名字往往包含多个字,所以这个概率相对是比较高的,这其实也是很符合我们直观认识的。
假设我们现在有个标签序列:B-Person, I-Person, O, O,B-Organization, I-Organization。那么这个序列的转移分数可按照如下方式计算:
\(Seq_t = T_{I-Person,B-Person} + T_{O,I-Person} + T_{O,O} + T_{O,B-Organization} + T_{B-Organization, I-Organization}\)
这个转移分数矩阵是CRF中的一个可学习的参数矩阵,它的存在能够帮助我们显示地去建模标签之间的转移关系,提高命名实体识别的准确率。
2.3 CRF建模的损失函数¶
前边我们讲到,CRF能够帮助我们以一种全局的方式建模,在所有可能的路径中选择效果最优,分数最高的那条路径。那么我们应该怎么去建模这个策略呢,下面我们来具体谈谈。
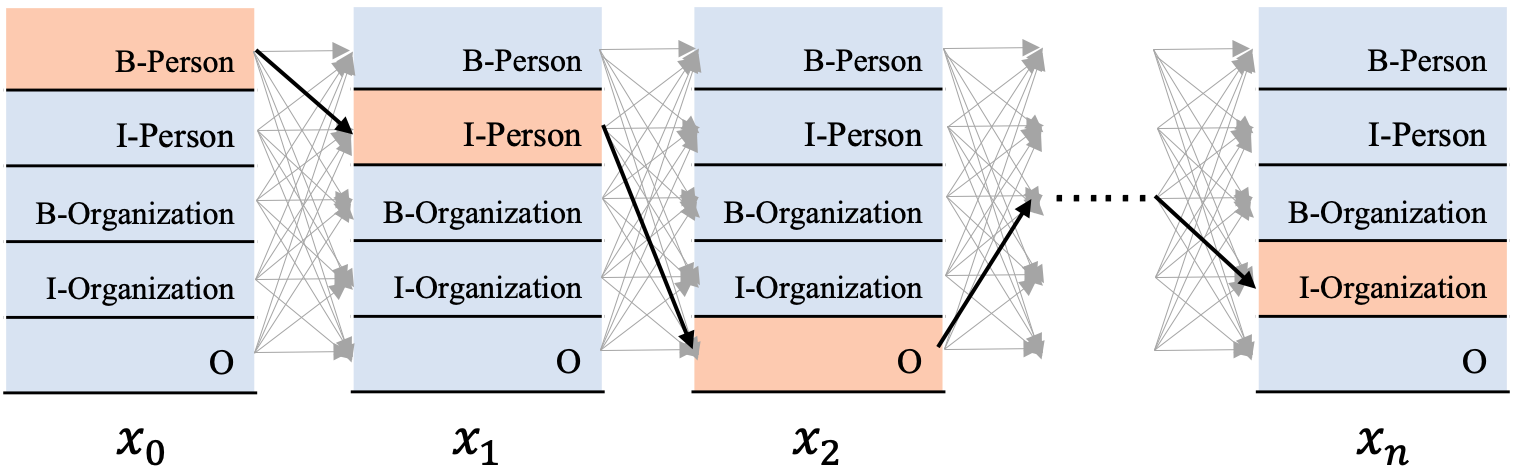
图5展示了CRF的工作图,现在我们有一串输入\(x=[x_0, x_1, x_2, x_n]\)(这里的\(x\)是文本串对应的发射分数,每个字词\(x_i\)都对应着一个发射分数向量,也就是前边提到的标签向量,该向量的维度就是标签数量),期待解码出相应的标签序列\(y=[y_0, y_1,y_2, ..., y_n]\),形式化为对应的条件概率公式如下:
在第2节我们提到,CRF的解码策略在所有可能的路径中,找出得出概率最大,效果最优的一条路径,那这个标签序列就是模型的输出,假设标签数量是\(k\),文本长度是\(n\),显然会有\(N=k^n\)条路径,若用\(S_i\)代表第\(i\)条路径的分数,那我们可以这样去算一个标签序列出现的概率:
现在我们有一条真实的路径\(real\),即我们期待CRF解码出来的序列就是这一条。那它的分数可以表示为\(s_{real}\),它出现的概率就是:
所以我们建模学习的目的就是为了不断的提高\(P(S_{real})\)的概率值,这就是我们的目标函数,当目标函数越大时,它对应的损失就应该越小,所以我们可以这样去建模它的损失函数:
为方便求解,我们一般将这样的损失放到log空间去求解,因为log函数本身是单调递增的,所以它并不影响我们去迭代优化损失函数。
千呼万唤始出来,这就是我们CRF建模的损失函数了。我们整个BiLSTM+CRF建模的目的就是为了让这个函数越来越小。从这个损失函数可以看出,这个损失函数包含两部分:单条真实路径的分数\(S_{real}\),归一化项\(log(e^{S_1}+e^{S_2}+...+e^{S_N})\),即将全部的路径分数进行\(log\_sum\_exp\)操作,即先将每条路径分数\(S_i\)进行\(exp(S_i)\),然后再将所有的项加起来,最后取\(log\)值。
讲到这里,有的同学可能会有疑惑,这里的每条路径分数应该怎么算呢?接下来,我们就来解决这个问题。
2.4 单条路径的分数计算¶
在开始之前,我们再来做一些约定,前边我们提到了发射分数和转移分数,假设\(E\)代表发射分数矩阵,\(T\)代表转移分数矩阵,\(n\)代表文本序列长度,\(tag\_size\)代表标签的数量。另外为方便书写,我们为每个标签编个id号(参考图5中涉及到的标签),如图6所示。

其中,\(E\)的shape为\([n, tag\_size]\),每行对应着一个文本字词的发射分数,每列代表一个标签,例如,\(E_{01}\)代表\(x_0\)取id为1的标签分数,\(E_{23}\)代表\(x_2\)取id为3的标签分数。\(T\)的shape为\([tag\_size, tag\_size]\),它代表了标签之间相互转移的分数,例如,\(T_{03}\)代表id为3的标签向id为0的标签转移分数。
每条路径的分数就是由对应的发射分数和转移分数组合而成的,对于图5标记出来的黄色路径来说,\(x_0\)的标签是B-Person,对应的发射分数是\(E_{00}\),\(x_1\)的标签是I-Person,对应的发射分数是\(E_{11}\),由B-Person向I-Person转移的分数是\(T_{10}\),因此到这一步的分数就是:\(E_{00}+T_{10}+E_{11}\)。
接下来\(x_2\)的标签是\(O\),由\(x_1\)的标签向I-Person向\(x_2\)的标签O转移的概率是\(T_{41}\),因此到这一步的分数是:\(E_{00}+T_{10}+E_{11}+T_{41}+E_{24}\),依次类推,我们可以计算完整条路径的分数。假设第\(i\)个位置对应的标签为\(y_i\),则整条路径的分数计算形式化公式为:
2.5 全部路径的分数计算¶
2.3节中的损失函数包括两项,单条真实路径分数的计算和归一化项(如上所述,全部路径分数的\(log\_sum\_exp\),为方便描述,后续直接将个归一化项描述为全部路径之和)的计算。这里你或许会问,现在知道了单条路径分数的计算方式,遍历一下所有的路径算个分数,不就可以轻松算出全部路径之和吗?是的,这在理论上是可行的。
但是,前边我们提到这个路径的数量是个指数级别的量纲,假设我对串包含50个字的文本串进行实体识别,标签的数量是31,那么这个路径的数量将是\(31^{50}\)条,这是真的是难以接受的一件事情,它会远远拖慢模型的训练和预测效率。
因此,我们要换一种高效的思路,这里其实用到了一种被称为前向算法的动态规划,它能帮助我们将图5所有路径的和计算,拆解为每个位置的和计算,最终得出所有的路径之和。如果这是你第一次听到这个算法,那也没关系,我会通过示例的方式,为你展现这个算法的工作原理,但是在看这部分内容之前,我们再来回顾一下我们的计算目标,即损失函数中的第1项:
另外,为方便描述这个原理,我们来简化下这个问题,假设我们现在在计算图7所示的所有路径之和。
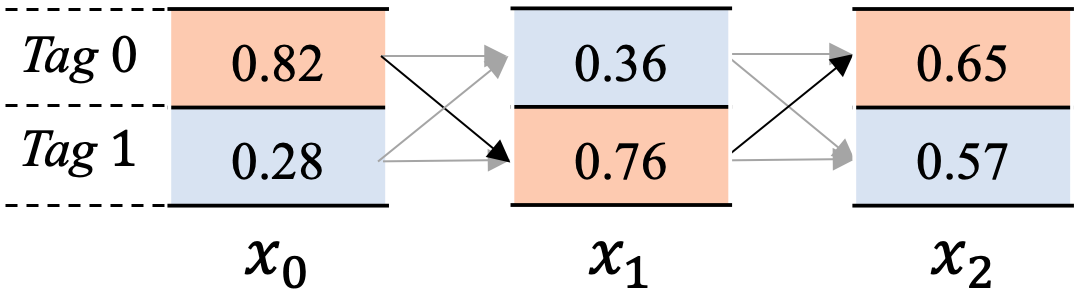
图7中,共包含2个标签\(Tag\) 0 和\(Tag\) 1, 文本串有3个单词\(x_0, x_1, x_2\)。我们再来做些约定如下:
\(emission_i=[x_{i0},x_{i1}]\), 代表\(x_i\)位置的发射分数。
其中,\(x_{i0}\)代表\(x_i\)位置输出\(Tag\) 0 标签的分数, \(x_{i1}\)代表\(x_i\)位置输出\(Tag\) 1 标签的分数。
\( trans = \left[ \begin{matrix} t_{00} & t_{01}\\ t_{10} & t_{11} \end{matrix} \right] \), 代表转移矩阵。
其中,\(t_{01}\)代表从\(Tag\) 1 转移到\(Tag\) 0的分数,\(t_{10}\)代表从\(Tag\) 0 转移到\(Tag\) 1的分数,依次类推。
\(alpha_i=[s_{i0},s_{i1}]\), 其中各个数值代表到当前位置\(x_i\)为止,以\(x_i\)位置相应标签结尾的路径分数之和。
以\(x_2\)步为例,\(alpha_2=[s_{20},s_{21}]\),其中\(s_{20}\)代表截止到\(x_2\)步骤为止,以标签\(Tag\) 0 结尾所有的路径分数之和,\(s_{21}\)代表截止到\(x_2\)步骤为止,以标签\(Tag\) 1结尾的所有路径分数之和。
这里比较抽象,如图7所示,参与\(x_2\)步的\(s_{20}\)分数计算的路径包括4条,即\(s_{20}\)是下边4条路径分数之和,依次如下
\(x_{00},x_{10},x_{20}\)
\(x_{00},x_{11},x_{20}\)
\(x_{01},x_{10},x_{20}\)
\(x_{01},x_{11},x_{20}\)
恭喜,我们完成了一些枯燥的定义,下边我们来看看如何计算所有路径的分数和吧,这里我们分成3步走来解释,首先计算截止到\(x_0\)位置,到各个标签的分数(上边的\(alpha\)内容)是多少;截止到\(x_1\)位置,到各个标签的分数是多少;截止到\(x_2\)位置,到各个标签的分数是多少。
第1步,截止到\(x_0\)位置
当前位置\(x_0\)输入的发射分数为:\(emission_0=[x_{00},x_{01}]\),因为这是序列的起始,显然截止到\(x_0\)位置有:\(alpha_0=[x_{00},x_{01}]\)。
截止到\(x_0\)这一步,将\(x_0\)位置的所有标签的分数累计作为所有路径的分数为:
第2步,截止到\(x_1\)位置
当前步骤涉及到\(x_0\)向\(x_1\)位置的转移,在这个过程中,\(x_1\)位置输入的发射分数为:\(emission_1=[x_{10}, x_{11}]\), 转移概率矩阵为: \( trans = \left[ \begin{matrix} t_{00} & t_{01}\\ t_{10} & t_{11} \end{matrix} \right] \), 前一个位置\(x_0\)各标签的路径累计和\(alpha_0=[x_{00},x_{01}]\)。
接下来我们expand一下\(emission_1\) 和 \(alpha_0\),力求通过矩阵计算的方式一次完成当前位置\(x_1\)各个标签的路径累计\(alpha_1\),具体如下:
然后我们来计算截止到\(x_1\)位置,到不同标签的每条路径的分数:
我们来看一条路径分数的计算,例如\( x_{00}+t_{10}+x_{11}\), 它代表在\(x_0\)的位置标签为\(Tag\) 0,在\(x_1\)的位置标签为\(Tag\) 1,然后通过加上\(t_{10}\)完成了\(x_0\)位置\(Tag\) 0标签 向 \(x_1\)位置标签\(Tag\) 1的转移。
从上边的结果可以看到,第1行代表向当前位置\(x_1\)标签\(Tag\) 0的转移路径,第2行代表向当前位置\(x_1\)标签\(Tag\) 1的转移路径。以第1行为例,将第1行的路径分数相加,就相当于到当前位置\(x_1\)并且以\(Tag\) 0结尾的所有路径之和。
因此,这样我们可以容易地算出当前位置\(x_1\)的各个标签的路径累计分数\(alpha_1\):
\(alpha_1 = [log(e^{x_{00}+t_{00}+x_{10}}+e^{x_{01}+t_{01}+x_{10}}), log(e^{x_{00}+t_{10}+x_{11}}+e^{x_{01}+t_{11}+x_{11}})]\)
最后,我们来算下截止到\(x_1\)位置,所有的路径和:
再回顾一下我们的计算目标:\(log(e^{S_1}+e^{S_2}+...+e^{S_N})\),你可以看到如果图7最终只到\(x_1\)位置,那么上边的这个结果就是我们相求的全部路径之和,或者说是归一化项。
第3步,截止到\(x_2\)位置
我们再来看下\(x_2\)位置的一些输入信息,\(x_2\)位置输入的发射分数为:\(emission_2=[x_{20}, x_{21}]\), 转移概率矩阵为: \( trans = \left[ \begin{matrix} t_{00} & t_{01}\\ t_{10} & t_{11} \end{matrix} \right] \), 前一个位置\(x_1\)各标签的路径累计和\(alpha_1=[log(e^{x_{00}+t_{00}+x_{10}}+e^{x_{01}+t_{01}+x_{10}}), log(e^{x_{00}+t_{10}+x_{11}}+e^{x_{01}+t_{11}+x_{11}})]\)。
接下来继续expand一下\(emission_2\) 和 \(alpha_1\),力求通过矩阵计算的方式一次完成当前位置\(x_2\)各个标签的路径累计\(alpha_2\),具体如下:
然后我们来计算截止到\(x_2\)位置,到不同标签的每条路径的分数:
继续按行累加,算出到当前位置\(x_2\)的各个标签的路径累计分数\(alpha_2\):
最后,我们来算下截止到\(x_2\)位置,所有的路径和:
显然,这个式子的结果就是最终我们想要的计算目标,损失函数中的第1项,共计包含8条路径的分数。
2.6 CRF的Viterbi解码¶
在前边几节,我们讲过了CRF的损失函数、单条路径分数的计算、全部路径分数的计算,根据这些内容完全可以进行BiLSTM+CRF的训练。但是,我们如何使用CRF从全部的路径中解码出得分最高的那条路径呢?
同2.5节所述,计算全部路径分数后,选择得分最大的那条路径肯定是不行的。其实这里是使用了一种被称为Viterbi的算法,它的思想和2.5节介绍的前向算法有些类似,将从全部路径中查找最优路径的过程,拆解为选择每个位置累计的最大路径。如果这是你第一次接触Viterbi算法,也不用担心,本节依然会通过示例的方式展现这个算法原理。
我们依然以图7为例,解码这全部路径中分数最大的这条(图中橙色显示的这条路径)。在正式介绍之前,我们依然做些约定如下:
\(emission_i=[x_{i0},x_{i1}]\), 代表\(x_i\)位置的发射分数。
其中,\(x_{i0}\)代表\(x_i\)位置输出\(Tag\) 0 标签的分数, \(x_{i1}\)代表\(x_i\)位置输出\(Tag\) 1 标签的分数。
\( trans = \left[ \begin{matrix} t_{00} & t_{01}\\ t_{10} & t_{11} \end{matrix} \right] \), 代表转移矩阵。
其中,\(t_{01}\)代表从\(Tag\) 1 转移到\(Tag\) 0的分数,\(t_{10}\)代表从\(Tag\) 0 转移到\(Tag\) 1的分数,依次类推。
\(alpha_i=[s_{i0},s_{i1}]\), 其中各个数值代表到当前位置\(x_i\)为止,以当前位置\(x_i\)相应标签结尾的路径中,取得最大分数的路径得分。
以\(x_2\)位置为例,\(alpha_2=[s_{20},s_{21}]\),其中\(s_{20}\)代表截止到\(x_2\)步骤为止,以标签\(Tag\) 0 结尾所有的路径中得分最大的路径分数,\(s_{21}\)代表截止到\(x_2\)步骤为止,以标签\(Tag\) 1结尾的所有路径中得分最大的路径分数。
这里比较抽象,如图7所示,参与\(x_2\)步的\(s_{20}\)分数计算的路径包括4条,\(s_{20}\)是这4条路径中得分最大这一条对应的分数,即下边这一条路径:\(x_{00},x_{11},x_{20}\)。
\(beta_i = [p_{i0},p_{i1}]\),其中各个数值代表到当前位置\(x_i\)为止,以当前位置\(x_i\)相应标签结尾的路径中,分数最大的那一条路径在前一个位置\(x_{i-1}\)的标签索引(每个标签对应的id号)。
以\(x_2\)位置为例,\(beta_2 = [p_{20},p_{21}]\),其中\(p_{20}\)代表代表截止到\(x_2\)步骤为止,以标签\(Tag\) 0 结尾所有的路径中得分最大的那条路径在\(x_{i-1}\)位置的标签索引,同理\(p_{21}\)代表截止到\(x_2\)步骤为止,以标签\(Tag\) 1结尾的最大路径在\(x_{i-1}\)位置的标签索引。
同样,如图7所示,在\(x_2\)位置,到标签\(Tag\) 0的所有路径中,分数最大的路径是:\(x_{00},x_{11},x_{20}\),因为前一个位置\(x_{i-1}\)的标签是\(Tag\) 1,因此\(p_{20}=1\)。
恭喜,我们又一次完成了这些枯燥的定义,下边我们来看看如何选择所有路径中得分最大的这一条吧,这里我们同样分成3步走来解释,首先计算截止到\(x_0\)位置,到各个标签的最大得分(上边的\(alpha\)内容)是多少;截止到\(x_1\)位置,到各个标签的最大得分是多少;截止到\(x_2\)位置,到各个标签的最大得分是多少。
第1步,截止到\(x_0\)位置
当前位置\(x_0\)输入的发射分数为:\(emission_0=[x_{00},x_{01}]\),因为这是序列的起始,显然截止到\(x_0\)位置有:\(alpha_0=[x_{00},x_{01}]\)
另外因为起始位置前边没有路径,这里我们使用-1来初始化:\(beta_0=[-1,-1]\)
第2步,截止到\(x_1\)位置
当前步骤涉及到\(x_0\)向\(x_1\)位置的转移,在这个过程中,\(x_1\)位置输入的发射分数为:\(emission_1=[x_{10}, x_{11}]\), 转移概率矩阵为: \( trans = \left[ \begin{matrix} t_{00} & t_{01}\\ t_{10} & t_{11} \end{matrix} \right] \), 到前一个位置\(x_0\)各标签的最大路径得分为\(alpha_0=[x_{00},x_{01}]\)。
接下来按照2.5节同样的方式,我们expand一下\(emission_1\) 和 \(alpha_0\),力求通过矩阵计算的方式一次完成到当前位置\(x_1\)各个标签的所有路径中得分最大的路径分数\(alpha_1\),具体如下:
然后我们来计算截止到\(x_1\)位置,到不同标签的每条路径的分数:
同样地,以第1行为例,第1行代表到当前位置\(x_1\)标签\(Tag\) 0结尾的所有路径的得分,那么第1行中分数最大这一条路径,就是到当前位置\(x_1\)并且以\(Tag\) 0结尾的所有路径中得分最大的路径。
因此,这样我们可以容易地算出到当前位置\(x_1\)的各个标签的最大路径分数\(alpha_1\):
显然从上边结果中,我们能够分析出到\(x_1\)位置各个标签的最大路径,例如到\(Tag \) 0的路径有\(x_{00}+t_{00}+x_{10}\) 和 \( x_{01}+t_{01}+x_{10}\), 其中较大者就是我们想要的到\(x_1\)位置 \(Tag \) 0的最大路径。
这里不妨我们做个假设:
\(x_{00}+t_{00}+x_{10} < x_{01}+t_{01}+x_{10}\)
\(x_{00}+t_{10}+x_{11} > x_{01}+t_{11}+x_{11}\)
因此,我们可以获得\(x_1\)位置的索引\(beta_1=[1,0]\),这代表在\(x_1\)位置,到标签\(Tag\) 0的最大路径的前一个位置\(x_{i-1}\)的标签是\(Tag\) 1, 到标签\(Tag\) 1的最大路径的前一个位置\(x_{i-1}\)的标签是\(Tag\) 0。
第3步,截止到\(x_2\)位置
我们再来看下\(x_2\)位置的一些输入信息,\(x_2\)位置输入的发射分数为:\(emission_2=[x_{20}, x_{21}]\), 转移概率矩阵为: \( trans = \left[ \begin{matrix} t_{00} & t_{01}\\ t_{10} & t_{11} \end{matrix} \right] \), 前一个位置\(x_1\)各标签的路径累计和:\(alpha_1=[max(x_{00}+t_{00}+x_{10}, x_{01}+t_{01}+x_{10}), max(x_{00}+t_{10}+x_{11}, x_{01}+t_{11}+x_{11})]\)。
接下来继续expand一下\(emission_2\) 和 \(alpha_1\),力求通过矩阵计算的方式一次完成当前位置\(x_2\)各个标签的路径累计\(alpha_2\),具体如下:
然后我们来计算截止到\(x_2\)位置,到不同标签的每条路径的分数:
因此,这样我们可以容易地算出到当前位置\(x_2\)的各个标签的最大路径分数\(alpha_2\):
这里我不妨再假设:
\(max(x_{00}+t_{00}+x_{10}, x_{01}+t_{01}+x_{10}) +t_{00}+x_{20} > max(x_{00}+t_{10}+x_{11}, x_{01}+t_{11}+x_{11})+t_{01}+x_{20})\)
\(max(x_{00}+t_{00}+x_{10}, x_{01}+t_{01}+x_{10})+t_{10}+x_{21} < max(x_{00}+t_{10}+x_{11}, x_{01}+t_{11}+x_{11}) +t_{11}+x_{21} )\)
上一步我们曾假设:
\(x_{00}+t_{00}+x_{10} < x_{01}+t_{01}+x_{10}\)
\(x_{00}+t_{10}+x_{11} > x_{01}+t_{11}+x_{11}\)
因此有:
\(x_{01}+t_{01}+x_{10}+t_{01}+x_{10} < x_{00}+t_{10}+x_{11}+t_{01}+x_{20}\)
\(x_{01}+t_{01}+x_{10}+t_{10}+x_{21} > x_{00}+t_{10}+x_{11}+t_{11}+x_{21}\)
所以\(x_2\)位置的索引:\(beta_2 = [1,0]\)
此时:\(alpha_1=[x_{00}+t_{10}+x_{11}+t_{01}+x_{20}, x_{01}+t_{01}+x_{10}+t_{10}+x_{21} ]\)
在图7中橘色路径分数最高,其对应的是\(x_{00}+t_{10}+x_{11}+t_{01}+x_{20}\),因此再假设:
\(x_{00}+t_{10}+x_{11}+t_{01}+x_{20} > x_{01}+t_{01}+x_{10}+t_{10}+x_{21}\)
这其实代表在\(x_2\)位置的所有标签对应的最大路径中,\(Tag\) 0 对应的那条路径是最大的,这条路径也是全局所有路径中分数最大的那一条,是我们要解析出的期望路径。
第4步,开始解码标签序列
到现在位置,我们通过\(beta_0\)记录下了最大路径上的节点,接下来我们可以通过回溯来找出全局所有路径中的最大路径。
首先,在\(x_2\)位置所有标签对应的最大路径中,\(Tag\) 0 对应的路径分数最大。因此\(x_2\)位置对应的标签就是\(Tag\) 0。
然后,\(beta_2 = [1,0]\),因此\(x_2\)位置解析出的标签\(Tag\) 0,对应的上一位置\(x_1\)的标签是\(Tag\) 1。
接下来,\(beta_1=[1,0]\),因此\(x_1\)位置解析出的标签\(Tag\) 1,对应的上一位置\(x_0\)的标签是\(Tag\) 0。
最后,\(beta_0=[-1,-1]\),当解析到这一步的时候,反回的标签肯定是-1,因此这个回溯过程也就结束了。
当回溯完成之后,将解析出的结果倒序排序,就是我们期望的最大路径。以图7为例,该路径就是\(Tag\) 0 –>\(Tag\) 1 –>\(Tag\) 0。
恭喜,看到这里,相信你已经懂得了CRF的核心原理。江湖虽路远,但总会再见,如对笔者的文章满意,还请多多支持。
3. Reference¶
[1] 邱锡鹏. 神经网络与深度学习[M]. 北京:机械工业出版社,2021.
[2] 吴飞. 人工智能导论:模型与算法[M]. 北京:高等教育出版社,2020.
[3] CRF Layer on the Top of BiLSTM