分组卷积(Group Convolution)¶
一、分组卷积提出背景¶
分组卷积(Group Convolution)最早出现在AlexNet[1]中。受限于当时的硬件资源,在AlexNet网络训练时,难以把整个网络全部放在一个GPU中进行训练,因此,作者将卷积运算分给多个GPU分别进行计算,最终把多个GPU的结果进行融合。因此分组卷积的概念应运而生。
二、分组卷积与标准卷积的区别¶
对于尺寸为 \(H_1\times{W_1}\times{C_1}\) 的输入矩阵,当标准卷积核的尺寸为 \(h_1\times{w_1}\times{C_1}\) ,共有 \(C_2\) 个标准卷积核时,标准卷积会对完整的输入数据进行运算,最终得到的输出矩阵尺寸为 \(H_2\times{W_2}\times{C_2}\) 。这里我们假设卷积运算前后的特征图尺寸保持不变,则上述过程可以展示为 图1 。
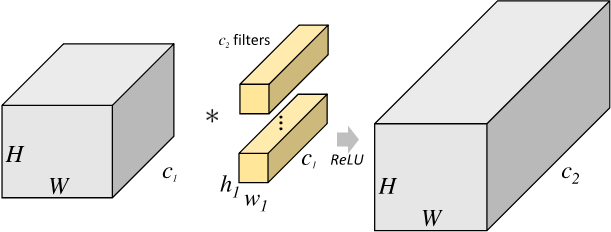
图1 标准卷积示意图
考虑到上述过程是完整运行在同一个设备上,这也对设备的性能提出了较高的要求。
分组卷积则是针对这一过程进行了改进。分组卷积中,通过指定组数 \(g\) 来确定分组数量,将输入数据分成 \(g\) 组。需要注意的是,这里的分组指的是在深度上进行分组,输入的宽和高保持不变,即将每 \(\frac{C_1}{g}\) 个通道的数据分为一组。因为输入数据发生了改变,相应的卷积核也需要进行对应的变化,即每个卷积核的输入通道数也就变为了 \(\frac{C_1}{g}\) ,而卷积核的大小是不需要改变的。同时,每组的卷积核个数也由原来的 \(C_2\) 变为 \(\frac{C_2}{g}\) 。对于每个组内的卷积运算,同样采用标准卷积运算的计算方式,这样就可以得到 \(g\) 组尺寸为 \(H_2\times{W_2}\times{\frac{C_2}{g}}\) 的输出矩阵,最终将这 \(g\) 组输出矩阵进行拼接就可以得到最终的结果。这样拼接完成后,最终的输出尺寸就可以保持不变,仍然是 \(H_2\times{W_2}\times{C_2}\) 。分组卷积的运算过程如 图2 所示。
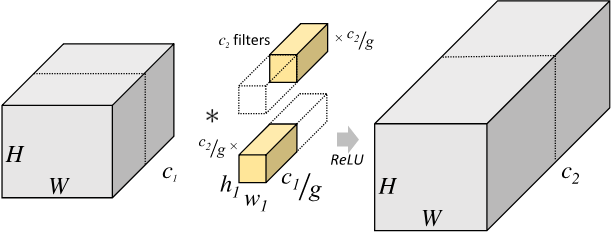
图2 分组卷积示意图
由于我们将整个标准卷积过程拆分成了 \(g\) 组规模更小的子运算来并行进行,所以最终降低了对运行设备的要求。同时,通过分组卷积的方式,参数量也可以得到降低。在上述的标准卷积中,参数量为:
而使用分组卷积后,参数量则变为:
三、应用示例¶
比如对于尺寸为 \(H\times{W}\times{64}\) 的输入矩阵,当标准卷积核的尺寸为 \(3\times{3}\times{64}\) ,共有 \(64\) 个标准卷积核时,图3 为组数 \(g=2\) 时的分组卷积计算方式。

图3 组数为2时分组卷积示意图
此时,每组的输入通道数变为32,卷积核通道数也变为为32。所以,标准卷积对应的参数量是 \(3\times{3}\times{64}\times{64}=36864\) ,而分组卷积的参数量变为 \(3\times{3}\times{32}\times{32}\times{2}=18432\),参数量减少了一半。